|
BOATBUILDING WITH A DIFFERENCE
III
(For Aspiring Amateurs)
by Barend Migchelsen Migchelsen@aol.com
https://ca.geocities.com/bmboats2002/
https://members.aol.com/_ht_a/migchelsen/myhomepage/
| Barend
Migchelsen,
(pronounced Mikkelsen) learned to sail in The Netherlands in 1943. In 1975 he started to
build boats and boat models as a hobby. Today, he organizes and teaches classroom
courses in boat building, and has published several books on the subject. The
following is an excerpt from one of these books. this is the second of
four parts.
|
|
STEMS
The meeting line fore and aft of the side panels of a
Double-ender is not just a curved line; the angle between the panels
varies from the sheer diminishing downward to the heel of the stem.
Its Profile view is shown in figure 3-1.
It makes construction of stems difficult for a new amateur who
has only beginners luck on his side. |
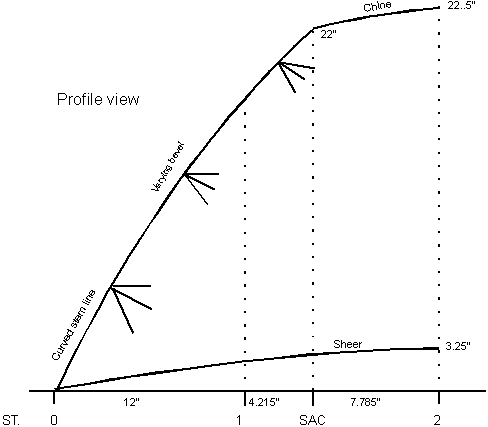
Fig. 3 - 1
The curved stem
has a varying crosscut angle.
The degree of variation over the whole stem can be
easily calculated, but it is a waste of time and effort unless you
insist on a curved stem.
Side
Panel Modification
From station #2 forward, and from station #14 toward
aft, the side panels are no longer bent, but are allowed to continue in
a straight direction as tangents to the sheer line circle segment.
Instead of coming together at station #0, the sheer
lines join each other five inches fore
of station #0 at the location #0-5", and aft at station #16+5". This
increases the Overall Length of the hull to LOA = 16', 10".
The angle that the tangent lines make with the
centerline is equal to the bevel angle of cross frame #2 (and #14),
which is equal to the angle of the center point angle between the radii
R2 and R8 (= the angle between R14 and R8).
That angle is 22.24 degrees.
See figure 3-2. |
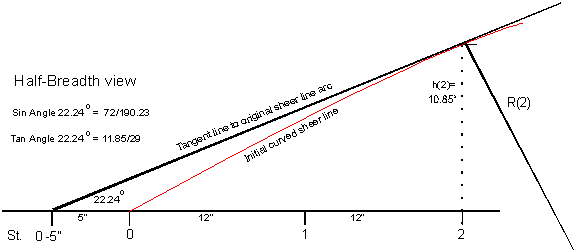
|
Fig. 3 - 2
Side panels
tangent line
Allowing the side panel to continue as the tangent
line to the sheer line arc delivers two important simplifications:
1.
The stem becomes straight.
2.
The bevel angle of the stem, called the crosscut angle becomes
constant.
What was the most difficult part to construct becomes
one of the easiest to cut, especially for the beginning amateur with
limited, or no carpenter’s skills at all.
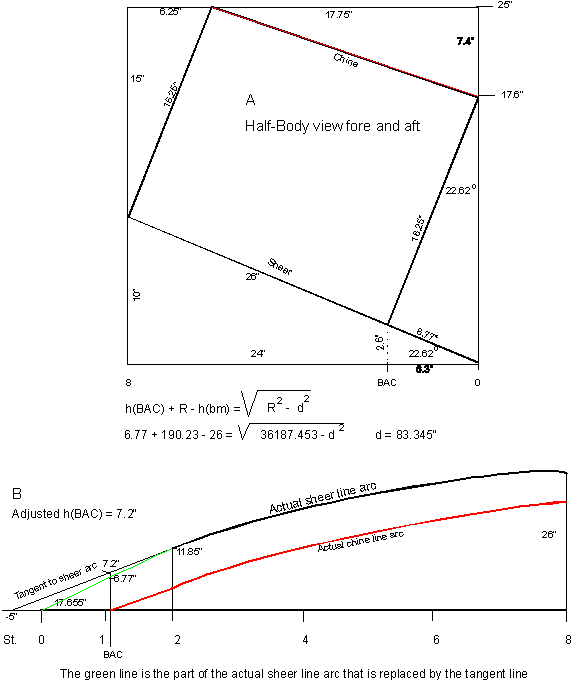
SAC
(Stem At Chine)
In figure 3-3, the Body view, the (maximum) bottom
rocker between Beam and the heel of the stems is three inches.
The location where the two chine lines join the heel of the stem I
call Stem At Chine.
For easy writing, abbreviated to SAC.
The location of Station SAC on the centerline is between stations #1 and #2.
See figure 3-1. On the sheer line in the half-Body view of figure 3-3 that
location is
hsac
= 22 x sin 22.62º = 22 x 0.3846 = 8.46”.
The exact location on the centerline of the station
line SAC in Profile and half Bread view can be calculated with the
formula:
hSAC
+ (R - hBeam) = v(R2 - dsac2), or 8.46 + (190.23 - 26) = v(190.232 -
dSAC2) in which dSAC
is the distance between station SAC and
station Beam (station #8).
Worked out, dSAC
= 79.785",
or the location of station
SAC = station #1 + 4.215" as is shown in figure 3-1, and more detailed
in figure 3-4. In this
illustration the original curved stem and the sheer line the Profile and
half-Breadth view are drawn in red.
The exact length, and the rake angle of the modified
stem in black lines are written in. Also
shown is how one half of the constant
crosscut is determined in this to
scale drawing. When the
drawing is made on one-inch-grid
graph paper a high degree of accuracy is achieved, even if it is done
on a one-quarter scale. It
makes the rest of the Profile and half-Breadth views redundant!
All the important values of the measurements are written in.
The mathematics is just Pythagoras and the basic
trigonometric definitions of Sine, Cosine, and Tangent applied.
It is all junior high school
stuff. If a check of the
accuracy of figures of these measurements gives you any difficulty, just
send me an email for clarification. |
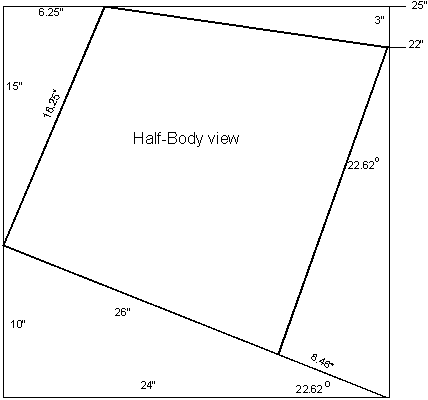
|
Fig. 3 - 3
Half- Body view
of the Double-Ender
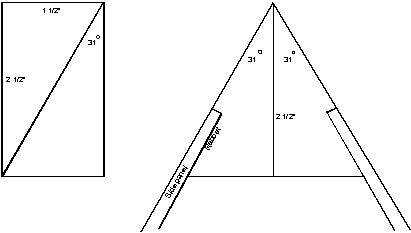
In figure 3-4, one-half of the crosscut angle is 31 degrees. A 2"x3"
ripped diagonally gives two right-triangular slats. The tangent of the angle between the hypotenuse/cut and the 2½"-long-leg
side is 1½/2½"
= 0.6. The angle is exactly
31 degrees! Place the two 2½" sides of the slats back to
back. Cut the rabbet
groove. Miter the stem at 46 degrees. In The
Netherlands, where I was born, they say:
“Even a toddler can do the washing.”
See figure 3-5.
With the modified sheer line, the straightened-out
stem, the raked tomb stone, or transom board, the increase of the
Overall Length, the added guardrails and their capping, varying flare
and the quoting of the outside measurements,
it becomes more difficult for the untrained eye to recognize the
original Double-Ender design from which the hull is developed. However, it is still there!
But the most important
result is that even a person with two left hands can now build the
simplified boat. |
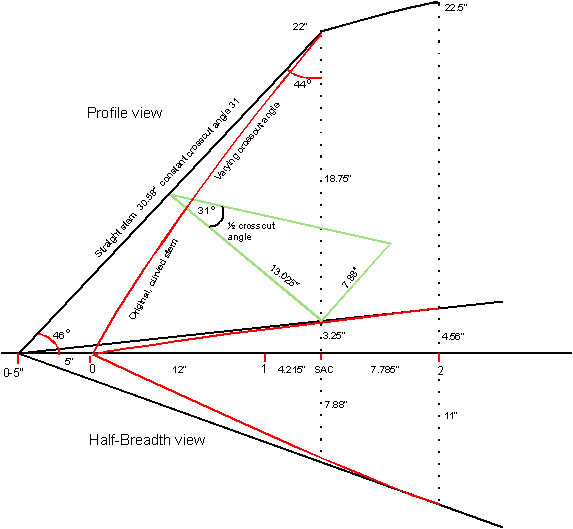
|
Fig. 3 - 4
Profile and Body view
of the modified stem |
|
Fig. 3 - 5
Stem made from diagonally ripped 2"x3"
Skiff
In a 12-ft Skiff the building of a hull is further
simplified by replacing the difficult-to-make stem aft with an even
easier-to-construct transom board.
A vertical transom board does not need any
modification of the original sheer line circle arc. The bevel angle of the board equals the center angle between
the radii R12 and R8 (Beam). The
distance between station #12 and station #8 is d12
= 48".
The sine of the center point angle is Sin CP-angle = d12/R = 48/190.23 = 0.252326. The center point angle is 14.6
degrees. The tangent of
that angle is: Tangent 14.6º = 0.26. Make a
right triangular template from a piece of scrap plywood.
The long leg is 10";
the short leg is 2.6". Set
the short leg on the table of the saw.
Adjust the blade against the hypotenuse.
Cut the bevel on the side of the transom.
I never bother to draw a transom, but take its measurements
directly from the setup. It
is foolproof.
Raked
Transom
Besides the fact that it makes the boat roomier, a
raked transom improves the beauty of the lines of the hull.
If the rake places the top edge of the transom between the sheers
at station #13, the sides of the transom board require the
difficult-to-make varying
bevel angle. This
difficulty is eliminated in the same way as with the stem fore:
From station #12 toward aft, the sides are allowed to go straight
in the direction of the tangent to the sheer line circle arc at station
#12. The varying bevel of the side edges is now the same constant
bevel of station #12 which is 14.6
degrees. It adds at the
most 1½" on each side at the width of the transom board between the sheer lines.
The width at the bottom at station #12 stays the same.
Especially with a raked transom, take measurements directly from
the setup.
FLARE
With flare, the bottom half of the boat is narrower.
Resistance when going through the water is reduced, the boat is
more stable when heeling, and the beauty of the lines of the boat is
enhanced.
Modern built dories all have varying flare.
But “classic” Dories, and the original Double-Enders from
which they were developed have constant flare. Flare
can vary between zero (0) degrees (no flare) to the maximum (Dory)
flare. A hull with no flare
at all is very easy to construct, but they are slow, and, IMHO, look
like overdue pregnant bathtubs. They
can also be dangerous when heeling.
When we speak of flare,
we actually mean flare ratio. In figure
3-3 the flare ratio is 6.25/15
= 0.416667.
The same ratio is shown in the right triangle of the sheer
line/hypotenuse with the half-Breadth long leg and the Profile height
short leg. The ratio here
is the same 10/24
= 0.416667.
In a constant flared
hull the flare ratio is always
Profile
height/half-Breadth.
In most of the designs of hard-chined hulls, the constant
flare ratio lies between the ratios 6/24 = 0.25
minimally and 14/24 = 0.583333 maximally. The
flare angle lies between 14 degrees and 30
degrees. The reason why the
ratio 10/24 was worked out is that with a constant half-Breadth of 24", the number
10" is
exactly in the middle of the series 6,
8, 10, 12, and 14 for
the Profile height figures. See
the table at the end.
It is easy to understand that when you make your own
boat, you have a lot of choices. The
ratio 6/24
provides a roomier cockpit on a wider bottom with less tenderness than
the ratio 14/24 which produces a faster boat on a narrower bottom.
The choice is yours. Your choice depends on what you want to do with the boat,
where you are going to use it, and any other personal preferences that
you may have.
Without a heavy load the Dory is very nimble.
Windage takes a big easy grip on the hull.
Good tracking is difficult without a skeg or keel.
The rowing position is awkward.
It requires either long oars, or the handles of the oars that are
right under the chin of a crewmember of average size.
The same
characteristics that made her an ideal fishing platform in the wide
ocean become disadvantages for the purpose of leisure boating in less
open waterways.
The first modification would have to be reducing of
the width of the side panels to provide a wider bottom, and a roomier
cockpit. The second change
has to be the attachment of a keel beam with a skeg.
This improves tracking. Both
modifications make rowing easier and make the boat more suitable for the
installation of a centerboard in a box and the rigging for sailing.
One more remark about this:
Whatever the modifications over time, the flare angle of the
original design can always be found at Beam.
Even in varying flare Dories and the Double-Enders from which
they are developed. See the
Dory picture.
To stay on the subject: Dories are designed as “fishing platforms”; sturdy boats
that stayed afloat under nearly all circumstances.
Their high sides give support to a bending-over fisherman trying
to grab the lines of the catch. The
boat can take a heavy load. They
are easily stacked aboard of the mother-ship/schooner.
The lack of a keel and a skeg let them drift gentle at the
fishing lines. The beauty
of the hull lines was, IMHO, an accidental quality.
Local weather and water conditions account for the
change of constant flare into varying flare. This gave more accent to
the fine cod’s head; mackerel
tail shape of the modern dories which is visible at the bottom.
The sheer line amidships did not change, but the side panels fore
and aft were allowed to follow the straight tangent line. The curve in the bow stem became less pronounced and is
easier to make because it diminished the varying bevel of the stem.
So was the bevel of the sides of the tombstone.
With these small changes, the development of the Dory shape had
reached the end of the line. See
the photograph of a new Lunenburg Dory beside The Dory Shop at the end
of the wharf of that city.
The
Dory flare angle is exactly 33.69
degrees, or 33º, 41', 24". I
picture the raised eyebrows and the big question marks in your eyes.
At first sight it looks
likes an extremely odd figure.
In realty it makes as much sense, and it is as easy to construct
as the 3",
4", and 5"
carpenters triangle. Make
the long leg of a right triangular plate 3",
and the short leg 2". (Making the template legs
6", and 4"
is easier). The flare ratio
of the Dory is 2/3 =
0.66667. The angle between the hypotenuse and the 3" long leg is then exactly 33.69º
= Dory flare angle.
The pronounced flare angle contributes strongly to the beauty of
the Dory lines. I have
serious doubts if even Don Elliot is aware of this Dory characteristic.
If
you are still not convinced: Check
the flare angle of the Beam cross frame of the official drawing of the
Lovell Dory. |

|
The flare
ratio = 2/3
was a (unconscious?) stroke of genius.
It made the setting up of the frames for the “classic”
constant flare extremely easy and accurate.
I have spoken with several professional Dory builders who were
not aware of this characteristic. The
older ones had received an elementary school education only, or, forced
by bad economic conditions, even less.
Sometimes, they were more real artists than simple boat-builders
anyhow.
THE
SYSTEM
In the first article of this series, it is shown that
all other hard-chined, constant flared hull forms easily can be
developed from the original drawing of the Double-Ender, and the
formula:
Tan
Flare Angle = Profile height/half-Breadth.
Calculating the radius of the sheer line circle arc
segment provided the key, and became the basis for determining all the
other measurements of a hull. With
the printed tables found here, that information is at your fingertips.
No need to make the calculations yourself.
The first table provides the radius R for all the
flare ratios from 1/24
up to the maximum Dory flare ratio 16/24. The second table is the calculation of the locations of the
station lines on the hypotenuse/ sheer line in the Body view for the
most common flare ratios from 6/24
up to 14/24. The use of the tables
will save you a lot of time and effort.
Table of the
Calculations of the radius R for the Different Flare Ratios
The
mathematical equation for the radius R
is: 2
x hBm x R = (½ LOA)2 + hBm2.
|
Prfl
Hght
(inches) |
Flare
Ratio |
Flare
Angle
(degrees) |
hBm
(inches) |
hBm2
|
(½
LOA)2
+ hBm2 |
Radius
(inches) |
| 0 |
0 |
0 |
24.00 |
576 |
9216
+ 576 |
204.00 |
| 1 |
1/24 |
2.39 |
24.02 |
577 |
9216 + 577 |
203.85 |
| 2 |
2/24 |
4.76 |
24.08 |
580 |
9216 + 580 |
203.40 |
| 3 |
3/24 |
7.13 |
24.19 |
585 |
9216 + 585 |
202.60 |
| 4 |
4/24 |
9.46 |
24.33 |
592 |
9216 + 592 |
201.56 |
| 5 |
5/24 |
11.77 |
24.52 |
601 |
9216
+ 601 |
200.22 |
| 6 |
6/24 |
14.04 |
24.74 |
612 |
9216 + 612 |
198.63 |
| 7 |
7/24 |
16.26 |
25.00 |
625 |
9216
+ 625 |
196.82 |
| 8 |
8/24 |
18.44 |
25.30 |
640 |
9216
+ 640 |
194.78 |
| 9 |
9/24 |
20.56 |
25.63 |
657 |
9216
+ 657 |
192.60 |
| 10 |
10/24 |
22.62 |
26.00 |
676 |
9216
+ 676 |
190.23 |
| 11 |
11/24 |
24.62 |
26.40 |
697 |
9216
+ 697 |
187.75 |
| 12 |
12/24 |
26.57 |
26.83 |
720 |
9216
+ 720 |
185.16 |
| 13 |
13/24 |
28.44 |
27.30 |
745 |
9216
+ 745 |
182.44 |
| 14 |
14/24 |
30.26 |
27.78 |
772 |
9216 + 772 |
179.77 |
| 15 |
15/24 |
32.00 |
28.30 |
801 |
9216 + 801 |
176.98 |
| 16 |
16/24 |
33.69 |
28.84 |
832 |
9216
+ 832 |
174.18 |
Flare ratio table for a hard-chined hull of a
Double-Ender: LOA
= 16 ft.
|
The
underlined figures in the table are the measurements of the Double-Ender
described in this chapter. On
the same side panel width, the flare ratio figures above the line make
the bottom wider. The
figures below the line will make the bottom of the boat narrower.
This ratio table saves you the trouble of having to make the
calculations yourself.
Offset
Table of Profile Heights and Half-Breadths
In
general, the designs of most constant-flared, hard-chined hulls have a
flare ratio between 6/24
(¼)
and 14/24 (7/12), or a flare angle between 14
(14.036)
degrees and 30¼ (30.256) degrees.
With
this in mind, the plotting table for the actual sheer line arc, and the offsets
of the Profile heights, and the half Breadths at the different
stations is a great time and labour saving tool.
The
table is based on the sheer line circle segment of the 16-feet
double-ender. The Profile
heights at Beam vary from 6 inches to 14
inches on a (constant) half-Breadth width of 24
inches. It lists the Body
view measurements of the hypotenuses hn of the sheer line circle arc at the stations #2 = #14, #4 = #12, #6 =
#10, and station #8 (Beam). ½ LOA = 96". The
distances dn
are between each station and station #8 (Beam)
All
the measurement figures in the table are given in inches.
The
mathematical equation is
hn = v(R2 - dn2) - (R - hBm).
|
Flare
Ratio |
R |
hBm |
h6
h10
d = 24 |
h4
h12
d = 48 |
h2
h14
d = 72 |
| 6/24 |
198.63 |
24.74 |
23.29 |
18.85 |
11.23 |
| 7/24 |
196.82 |
25.00 |
23.53 |
19.00 |
11.36 |
| 8/24 |
194.78 |
25.30 |
23.81 |
19.23 |
11.50 |
| 9/24 |
192.60 |
25.63 |
24.13 |
19.55 |
11.67 |
| 10/24 |
190.23 |
26.00 |
24.48 |
19.84 |
11.85 |
| 11/24 |
187.75 |
26.40 |
24.91 |
20.16 |
12.04 |
| 12/24 |
185.16 |
26.83 |
25.27 |
20.50 |
12.26 |
| 13/24 |
182.44 |
27.30 |
25.71 |
20.87 |
12.49 |
| 14/24 |
179.77 |
27.78 |
26.17 |
21.25 |
12.73 |
|
The underlined figures are the measurements of the
Double-Ender model constructed in these articles.
The Flare Ratio Table on the preceding page, and the
plotting table for the heights of the sheer line circle arc segment
above, eliminate the need to make any calculations.
Plot the dimensions on one-inch-grid graph paper.
Draw the hull lines completely in Body view.
Instead of the 10" Profile height at Beam as found in these
articles, change to the Profile height of your
choice, which can be any number between 6
inches, and 14 inches.
If you want to build a bigger boat, based on an 18', or 24'
Double-Ender, just increase the scale of all
the measurements by the factor 1½,
or 2. It is that simple with
this mathematical system of
design.
SIDE
PANELS
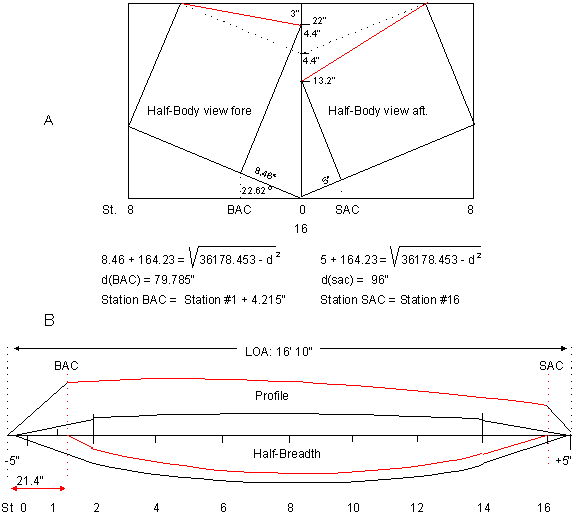
In
the half-Body view of a Double-Ender, figure3-6A, the chine line is
drawn parallel to the sheer line. The
side panels have the same width over the whole length.
The rocker from the Beam to the stems is 7.4".
Station BAC (Bow At Chine) has moved forward
to station #1 + 0.655”. The
chine lines in Plan and half-Breadth view run parallel to the sheer
lines. This strong rocker
is still visible in the McKenzie-River Dories. |
|
Fig. 3 - 6
Chine lines
parallel to the sheer lines
Cod’s
Head, Mackerel Tail
In figure 3 -7A, the original chine lines parallel to
the sheer lines are the dotted lines.
In this drawing a new chine line is drawn in red.
Instead of a rocker fore of Beam of 7.4", this rocker is reduced to 3", a
difference of 4.4".
At the same time the rocker aft of Beam is increased by the same amount of 4.4”.
The bottom is no longer parallel to the (horizontal)
plane of the two sheer lines, but tilted from fore to aft as shown in
the Profile drawing of figure 3-7B.
Although the sheer line
itself has not changed, the bow has become substantially higher. (or
should I say the bottom fore deeper?)
In Dories this is not so pronounced as in the Punter, but still
clearly visible in the photograph of the Dory in this posting. |
|
Fig.
3 - 7 Cod’s Head, Mackerel Tail
Figure
3-7B shows how this modification changes the contour of the bottom/chine
line. Station
BAC is now located at station #1
+ 4.215".
This station has moved aft. At
the same time Station SAC moved over to station line #16.
The worked out formulas under the figures3-6A and 3-7A show exactly
over what distance the movement took place.
Reflections
The effect of tilting the bottom with regards to the
(horizontal) sheer line plane is the very fine cod’s head; mackerel tail shape of the bottom that we find in
classic Double-Ender, Dories, and also in the Dutch Punters.
You can see this in the Punter that took fourth place in the design
competition of this magazine in the February edition of this year.
Until I made the drawings and the calculations, I
never consciously realized that it is only
the bottom shape that is modified.
In modern dories with varying flare it is more accentuated
because it moves the Beam of the bottom panel farther forward to station
#7.
Besides the
straightening-out of the sheer lines fore
of station line #2 and aft of
station line #14, the sheer line kept its original circle arc shape
between these two stations.
The fishermen of the American east coast, and of the
Zuiderzee in The Netherlands had good reasons to prefer hulls of this
shape that stands up against rough weather, and made fishing easier over
the lower end aft.
What I find remarkable is that the modern racing
yachts have practically exactly the same shape as these classic craft but
then 180 degrees reversed: The
mackerel tail is at the bow fore, the cod’s head is the stern aft.
Here, speed is more important than comfort.
On the other hand, this is a design that is found
also, and stands up to the sometimes very rough waters along the west
coast of Denmark where the big north-western storms from the North Sea run
dead against that Danish coast and the German north coast, the so-called Spitsgats
(translated literally: Pointy
Arses). . These boats have an excellent sea-boat reputation.
Conclusions
If this series of postings has given you a more
rounded insight in the process of designing, lofting, and construction of
hard-chined, small craft, give the credit to the great Guru of American
small craft observations, the late John Gardner.
His remarks pointed me in the right direction.
Once you have digested the simple system of designing
and lofting, you will find that it works much faster and far more
accurately than working with offset tables for the design of hard chined
hulls. It became possible
because of the invention of the pocket calculator.
But that is
also its drawback. I have not found a simple
method yet that can be applied to the design of hulls with compounded
lines and/or rounded side panels. Perhaps,
for this more complicated problem we need the PC with its expensive
software after all. Unless
… hopefully, there is a genius in our readers’ circle that has found,
or can develop a similar simple solution for these types of craft.
At least, I am dying to hear about it.
When that becomes possible, many more amateurs will
join our ranks. The lakes will become alive with sails, to steal, and
paraphrase a slogan from the Sound
of Music.
In the meantime, the aspiring amateurs who try, and
become familiar with the system
will find themselves well equipped for tackling the more complicated
problems successfully.
Sheers
and Chines, Barend. |

|
![]()